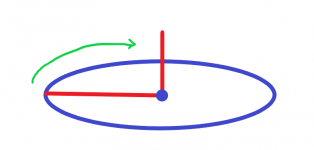
If you want an arc, you can try rotating a location around an axis in a loop for a certain amount of times.
How you would go about doing this is to have a location origin, vector axis, and a vector that is the vector to the particle, as well as an auxiliary location for the actual particle location.
Here's an example pseudocode:
C-like:
// some starting values that will define our arc
pfx = (whatever particle)
origin = Location (25.5, 51.5, 25.5)
axis = Vector (0, 1, 0)
vec = Vector (3, 0, 0)
degrees = Number 90
// drawing the arc
repeat Multiple(degrees) {
pos = ShiftOnVector(origin, vec)
DisplayParticle(pfx, pos)
vec = RotateVectorAroundVector(vec, axis, -1) // -1, because vectors rotate counterclockwise
}
pos = ShiftOnVector(origin, vec)
DisplayParticle(pfx, pos)
This code would create a 90 degree particle arc from (28.5, 51.5, 25.5) to (25.5, 51.5, 28.5), parallel to the ground.
pfx - that's the particle effect you want to display
origin - this is where the center of the arc is. It'd be the center of the circle, if you were to fully complete the arc
axis - this is the direction the arc is facing. (0, 1, 0) means move 0 along the x axis, move 1 along the y axis (upwards), and move 0 along the z axis (x and z being the horizontal); think of it as a line that goes straight through the center of the circle perpendicularly
vec - this is basically a ray that rotates around the axis
degrees - the number of degrees to rotate, of course
View attachment 1045